Time-Lapse Observation
このビデオは、我々の研究室で人工的に培養されたニューロンが、自発的にお互いに結合して複雑なネットワークを形成する過程を示しています。培養は多電極アレイ(MEA)上で行われており、光学顕微鏡で観察しながら同時に各電極から電気信号を検出することができます。多電極アレイを用いたこれまでの多くの研究から、ニューラルネットワークの大きな特徴は、同期バーストと呼ばれる現象を自発的に生ずることであることが分かっています。同期バーストは、哺乳動物の生体内でも観測されており、ニューラルネットワークの形成や高次脳機能にも関係していると考えられています。
我々の研究室では、同期バーストに対して、長期培養手法、蛍光イメージング、パターニング、光学顕微鏡・電子顕微鏡相関イメージング、遺伝子発現、スクリーニング、麻酔、低温保存、そして理論的解析等の観点から研究を進めています。
Fluorescence Imaging
Single Neuron
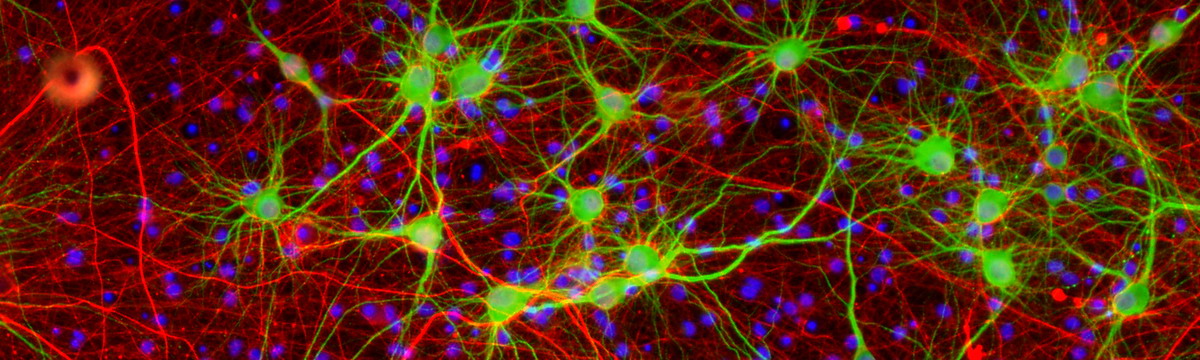
このビデオは、共焦点光学顕微鏡によって計測した、培養した単一ニューロンの3次元イメージングです。ニューロンは、MAP2 (blue)、VGAT (green)、VGluT1 (red)の3種類が免疫蛍光染色されています。興奮性・抑制性のシナプス結合の分布と密度などを定量化することができます。
Networks

(Ito D., et al., Neuroscience, 171(1), 2010. By courtesy of the IBRO.)
多電極上で培養されたニューラルネットワークを、蛍光顕微鏡により観察することは、ネットワークの空間的な構造を解析するために有効な方法です。図は、インパルスの電気信号を計測した直後に免疫化学法を施して観察された、免疫蛍光染色イメージの例を示しています(論文誌Neuroscienceの表紙を飾りました)。このイメージから、成長したニューラルネットワークに関する形態的な情報が得られます。
Cell Patterning

十分な電気信号のシグナルを得るために、多電極上で高い密度で培養することが一般的に行われています。しかし、電極上のニューロンは限定されているにも関わらず、電極上以外のニューロンから回り込む信号も混在するために、信号の解析が困難になります。そこで、我々は、人工的なニューロンの回路を形成させるパターニング手法について研究を進めています。図は、ニューラルネットワークが格子上に配置するようにパターニングされた多電極を用いて培養を行い、電気信号計測直後に得られた免疫蛍光染色イメージです。このようにパターニングされた培養系においても、同期バーストが観測されることを実証しました。パターニングは、同期バースト解析のためのプラットフォームとなることが期待されます。
Correlative Imaging of Optical and Electron microscopes
光学顕微鏡と電子顕微鏡を併用することは、生命現象を解き明かすための効果的な実験的手法であり、相関イメージングと呼ばれ、近年急速に研究が進展しています。このビデオは、その一例を示しています。単一のニューロンの軸索が成長している様子を、培養液中で光学顕微鏡によって観察しています。続いて、免疫化学的処理を施し、蛍光顕微鏡によって記録しました。最後に、真空中で、SEM(走査型電子顕微鏡)によって観察しました。光学顕微鏡と電子顕微鏡をシームレスに接続できていることが良く分かります。
Synchronized Burst
多電極アレイ(MEA)による培養によって、ニューラルネットワークの同期バーストは極めて多様な時空間パターンを示す事が明らかにされています。同期バーストとは、スパイクが密に集中した“バースト”が、異なるチャネルで一斉に“同期”する現象です。このビデオはその例を示しています。同期バーストは、ニューロンが互いに結合したニューラルネットワークの基本的な特徴なのです。
Theoretical Analysis
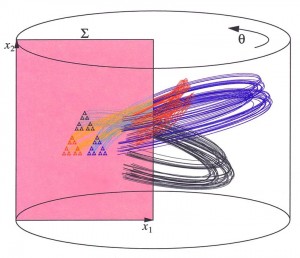
力学系とは、微分方程式または差分方程式を理論的に取り扱う学問体系であり、非線形動力学系、カオス力学系、ダイナミカルシステムなどと呼ばれることもあります。創始者はポアンカレ(Jules Henri Poincare, France, 1854~1912)であり、3つの星の運動を記述する運動方程式は『解析的に解くことは不可能』であることを数学的に証明する過程で、現在の力学系の基礎を築いたと言われています。このように力学系はその出発点からして古典力学との関係は深いのですが、現在では物理的な“力”を扱うのみならず、微分方程式または差分方程式で表される対象全てにかかわる基本的な学問として発展しています。ニューロンのインパルスは、4つの微分方程式で表現されることが知られており(A. L. Hodgkin & A. F. Huxley, 1952, 1963年ノーベル賞)、脳も力学系の対象と考えることができます。
本研究室では、多電極アレイによって得られた膨大な時系列データに対して、力学系を基本とした解析を進めています。
References
- D. Ito, T. Komatsu, K. Gohara:
Measurement of saturation processes in glutamatergic and GABAergic synapse densities during long-term development of cultured rat cortical networks,
Brain Research, 1534, 22-32, 2013.
doi: 10.1016/j.brainres.2013.08.004 - M. Suzuki, K. Ikeda, M. Yamaguchi, S. N. Kudoh, K. Yokoyama, R. Satoh, D. Ito, M. Nagayama, T. Uchida, K. Gohara:
Neuronal cell patterning on a multi-electrode array for a network analysis platform,
Biomaterials, 34(21), 5210-5217, 2013.
doi:10.1016/j.biomaterials.2013.03.042 - T. Uchida, S. Suzuki, Y. Hirano, D. Ito, M. Nagayama, and K. Gohara:
Xenon-induced inhibition of synchronized bursts in a rat cortical neuronal network,
Neuroscience, 214, 149-158, 2012.
doi:10.1016/j.neuroscience.2012.03.063 - T. Uchida, M. Nagayama, T. Taira, K. Shimizu, M. Sakai, K. Gohara:
Optimal temperature range for low-temperature preservation f dissociated neonatal rat cardiomyocytes,
Cryobiology, 63(3), 279-284, 2011.
doi:10.1016/j.cryobiol.2011.09.141 - M. Yamaguchi, K. Ikeda, M. Suzuki, A. Kiyohara, S. Kudoh, K. Shimizu, T. Taira, D. Ito, T. Uchida, and K. Gohara:
Cell patterning using a template of microstructured organosilane layer fabricated by vacuum ultraviolet light lithography,
Langmuir, 27 (20), 12521–12532, 2011.
doi: 10.1021/la202904g - D. Ito, H. Tamate, M. Nagayama, T. Uchida, S. Kudoh, and K. Gohara:
Minimum neuron density for synchronized bursts in a rat cortical culture on multi-electrode arrays,
Neuroscience, 171(1), 50-61, 2010.
doi:10.1016/j.neuroscience.2010.08.038 - Masaki Nomura, Daisuke Ito, Hiroki Tamate, Kazutoshi Gohara and Toshio Aoyagi:
Estimation of functional connectivity that causes burst-like population activities,
FORMA, 24(1), pp.11-16, 2009. - J. Nishikawa and K. Gohara:
Automata on Fractal Sets Observed in Hybrid Dynamical Systems,
Int, J. Bifurcation and Chaos, 18(12), pp.3665-3678, 2008.
doi:10.1142/S0218127408022639 - J. Nishikawa and K. Gohara:
Anomaly of fractal dimensions observed in stochastically switched systems,
Physical Review E, 77, 036210.1-036210. 8, 2008.
doi:10.1103/PhysRevE.77.036210 - H. Oka and K. Gohara:
Approximation of Fractal Transition Using Attractors Excited by Periodic Inputs,
Int. J. Bifurcation and Chaos, 13(4), pp.943-950, 2003.
doi:10.1142/S0218127403007059 - J. Nishikawa and K. Gohara:
Fractals in an Electronic Circuit Driven by Switching Inputs,
Int. J. Bifurcation and Chaos12(4), pp.827-834, 2002.
doi:10.1142/S0218127402004772 - R. Wada and K. Gohara:
Closures of Fractal Sets in Nonlinear Dynamical Systems with Switched Inputs,
Int. J. Bifurcation and Chaos, 11(8), pp.2205-2215, 2001.
doi:10.1142/S0218127401003395 - R. Wada and K. Gohara:
Fractals and Closures of Linear Dynamical Systems Excited Stochastically by Temporal Inputs,
Int. J. Bifurcation and Chaos,11(3), pp.755-779, 2001.
doi:10.1142/S0218127401002602 - S. Sato and K. Gohara:
Fractal Transition in Continuous Recurrent Neural Networks,
Int. J. Bifurcation and Chaos, 11(2), pp.421-434, 2001.
doi:10.1142/S0218127401002158 - S. Sato and K. Gohara:
Poincare Mapping of Continuous Recurrent Neural Networks Excited by Temporal External Input,
Int. J. Bifurcation and Chaos 10(7), pp.1677-1695, 2000.
doi:10.1142/S0218127400001055 - K. Gohara, H. Sakurai, and S. Sato:
Experimental Verification for Fractal Transition Using a Forced Damped Oscillator,
Fractals, 8(1), pp.67-72, 2000.
doi:10.1142/S0218348X00000081 - K. Gohara and A. Okuyama:
Fractal Transition -Hierarchical Structure and Noise Effect,
Fractals, 7(3), pp.313-326, 1999.
doi:10.1142/S0218348X99000311 - K. Gohara and A. Okuyama:
Dynamical Systems Excited by Temporal Inputs,
Fractals, 7(2), pp.205-220, 1999.
doi:10.1142/S0218348X99000220